Mathematics: Analysis and Approaches (SL & HL)
Nature of the Subject
Mathematics has been described as the study of structure, order and relation that has evolved from the practices of counting, measuring and describing objects. Mathematics provides a unique language to describe, explore and communicate the nature of the world we live in as well as being a constantly building body of knowledge and truth in itself that is distinctive in its certainty. These two aspects of mathematics, a discipline that is studied for its intrinsic pleasure and a means to explore and understand the world we live in, are both separate yet closely linked.
Mathematics is driven by abstract concepts and generalization. This mathematics is drawn out of ideas, and develops through linking these ideas and developing new ones. These mathematical ideas may have no immediate practical application. Doing such mathematics is about digging deeper to increase mathematical knowledge and truth. The new knowledge is presented in the form of theorems that have been built from axioms and logical mathematical arguments and a theorem is only accepted as true when it has been proven. The body of knowledge that makes up mathematics is not fixed; it has grown during human history and is growing at an increasing rate.
The side of mathematics that is based on describing our world and solving practical problems is often carried out in the context of another area of study. Mathematics is used in a diverse range of disciplines as both a language and a tool to explore the universe; alongside this its applications include analyzing trends, making predictions, quantifying risk, exploring relationships and interdependence.
While these two different facets of mathematics may seem separate, they are often deeply connected. When mathematics is developed, history has taught us that a seemingly obscure, abstract mathematical theorem or fact may in time be highly significant. On the other hand, much mathematics is developed in response to the needs of other disciplines.
The two mathematics courses available to Diploma Programme (DP) students express both the differences that exist in mathematics described above and the connections between them. These two courses might approach mathematics from different perspectives, but they are connected by the same mathematical body of knowledge, ways of thinking and approaches to problems. The differences in the courses may also be related to the types of tools, for instance technology, that are used to solve abstract or practical problems. The next section will describe in more detail the two available courses.
Distinction between Higher and Standard Level
Students who choose Mathematics: analysis and approaches at SL or HL should be comfortable in the manipulation of algebraic expressions and enjoy the recognition of patterns and understand the mathematical generalization of these patterns. Students who wish to take Mathematics: analysis and approaches at higher level will have strong algebraic skills and the ability to understand simple proof. They will be students who enjoy spending time with problems and get pleasure and satisfaction from solving challenging problems.
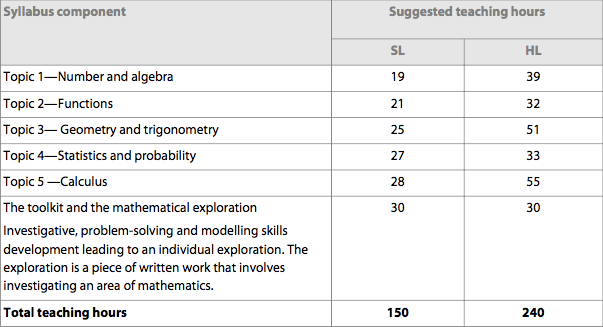
Course Content
Objectives
Having followed the Diploma Programme course in Mathematics, Analysis and Approaches, students will be expected to:
- Recall, select and use their knowledge of mathematical facts, concepts and techniques in a variety of familiar and unfamiliar contexts.
- Recall, select and use their knowledge of mathematical skills, results and models in both abstract and real-world contexts to solve problems.
- Transform common realistic contexts into mathematics; comment on the context; sketch or draw mathematical diagrams, graphs or constructions both on paper and using technology; record methods, solutions and conclusions using standardized notation; use appropriate notation and terminology.
- Use technology accurately, appropriately and efficiently both to explore new ideas and to solve problems.
- Construct mathematical arguments through use of precise statements, logical deduction and inference and by the manipulation of mathematical expressions.
- Investigate unfamiliar situations, both abstract and from the real world, involving organizing and analyzing information, making conjectures, drawing conclusions, and testing their validity.
Teaching Approach
Despite the attitude that mathematics is all around us and everything can be described through its use this structural interconnection of mathematics and real-world is neither self-evident nor easily established. Let us call the process of translating a real-world problem into mathematics mathematicalization. The students should be introduced into mathematicalization slowly, progressively, methodically and systematically passing from very simple examples/cases to more complex ones. The variety of topics in the syllabus creates a conducive environment to this end.
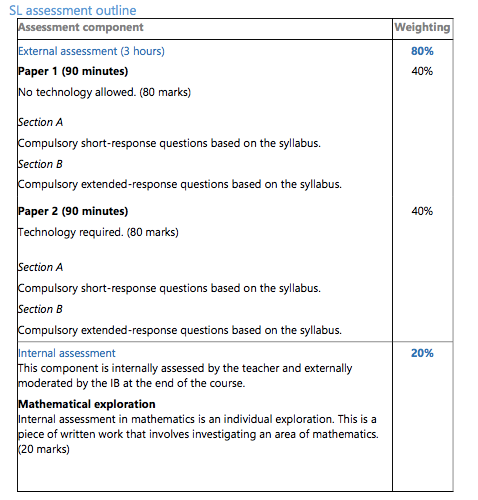
Assessment